Simulate Time-integrated Coarse-grained Molecular Dynamics with Multi-scale Graph Networks

Xiang Fu¹*, Tian Xie¹*, Nathan J. Rebello², Bradley D. Olsen², Tommi Jaakkola^1
1MIT CSAIL   ²Department of Chemical Engineering, MIT   *Equal Contribution
APS March Meeting 2022
ICLR 2022 DGM4HSD Workshop
MRS Spring Meeting 2022
[paper] [code]

Video

Abstract

Molecular dynamics (MD) simulation is the workhorse of various scientific domains but is limited by high computational cost. Learning-based force fields have made major progress in accelerating ab-initio MD simulation but are still not fast enough for many real-world applications that require long-time MD simulation. In this paper, we adopt a different machine learning approach where we coarse-grain a physical system using graph clustering and model the system evolution with a very large time-integration step using graph neural networks. A novel score-based GNN refinement module resolves the long-standing challenge of long-time simulation instability. Despite only being trained with short MD trajectory data, our learned simulator can generalize to unseen novel systems, and simulate for much longer than the training trajectories. Properties requiring 10-100 ns level long-time dynamics can be accurately recovered at several orders of magnitude higher speed than classical force fields. We demonstrate the effectiveness of our method on two realistic complex systems: (1) single-chain coarse-grained polymers in implicit solvent; (2) multi-component Li-ion polymer electrolyte systems.

Why ML simulator?

Molecular dynamics is often extremely complex. In graphics we can already simulate very realistic-looking water in very fast speed, but simulating realistic water in the MD sense is very difficult – not to mention more complex systems. For complex systems such as the polymers and batteries studied here, ab-initio MD based on quantum mechanics are simply computationally infeasible. People have designed amazing classical force fields to simulate such systems, but even with classical force fields some simulations (e.g., protein folding) are still too expensive.

ML force fields (FFs) have achieved significant progress in recent years. They can learn from ab-initio MD data and be orders of magnitude faster, without compromising accuracy. Huge potential is in ML methods to transform scientific computing!

Why time-integration with acceleration prediction?

Despite the success of ML FFs in simulating ab-initio MD, they are still not applied to more complex systems where ab-initio MD simulation is infeasible. And afterall an ML force field is still a force field. Simulation using a force field is fundamentally limited in its time-integration time – usually at femtosecond level for MD. However, useful properties can often require very long time simulation to obtain. E.g., protein folding and unfolding are rare events that require long simulation to capture.

Do we care about the detail dynamics up to femtosecond precision? Usually the answer is NO. This leads to the question: can we use a larger time-integration? Our take is to estimate the effect of forces integrated through a longer time interval: the time-integrated acceleration. Analytically this is certainly a very complex object. But with NN approximators, this complex object may in fact be learnable.

Why coarse-graining?

Coarse-graining models are widely used for accelerating MD simulations. When the properties we care about are at a “mesoscale” that we can afford losing some fine details in the dynamics, coarse-graining becomes very reasonable. Many estimation problems for complex systems fall into this regime. But for a ML simulator, the benefit is not just better speed.

Coarse-graining almost surely loses information and simplifies the dynamics being studied. The CG MD system is thus an easier target to learn for an ML simulator. In our study, we find this simplification is what makes the GNN simulator to work at all. The reduction in the degree of freemdom that the model needs to learn is massive. The spatial coarse graining also interacts with the teomporal time-integration: CG models often admit larger time-integration in the FF setting, and this also applies in our study.

How does the coarse-graining work?

Visualizing the coarse-graining process. (a) The full atomic-level dynamics of an example SPE. color code represents atomic number. (b) Still full atomic-level dynamics, but color coded with the component an atom belongs to: grey for polymer, blue for TFSI-ion, and yellow for Li-ion. (c) Color code the atoms with the CG-bead that the atom belongs to. (d) The SPE system after coarse-graining, where the color matches the previous atomic-level assignment. (e) The resulting coarse-grained system with color coding the component of each CG-bead: grey for polymer, blue for TFSI-ion, and yellow for Li-ion.

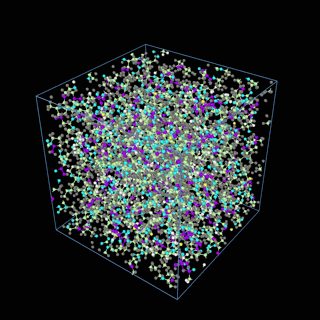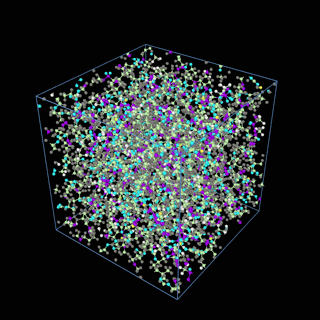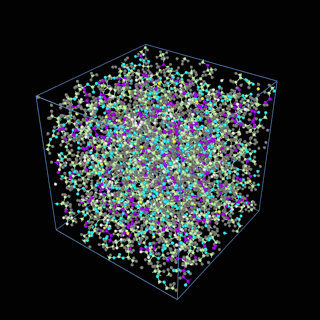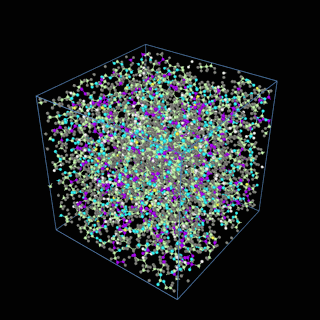
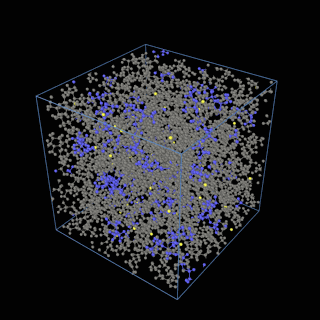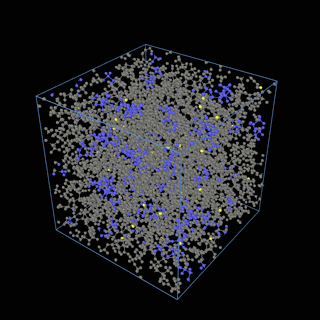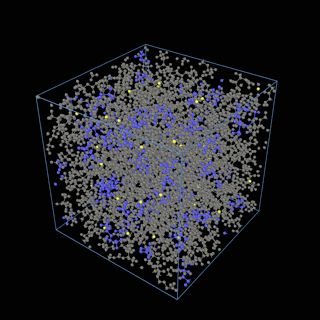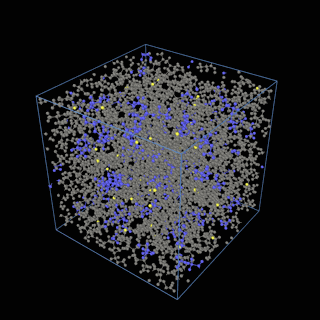
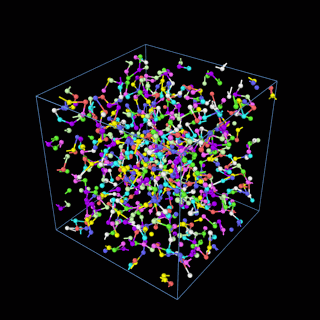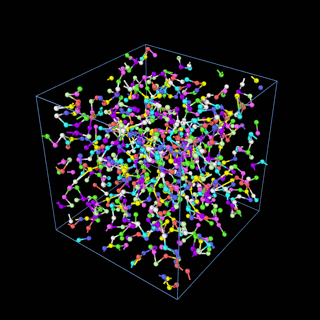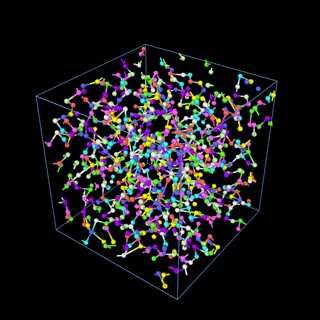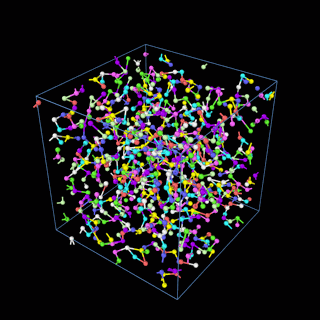
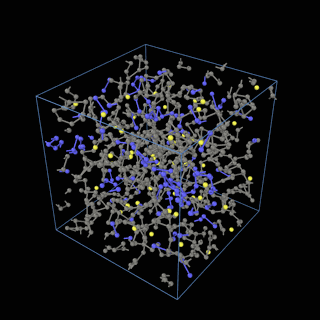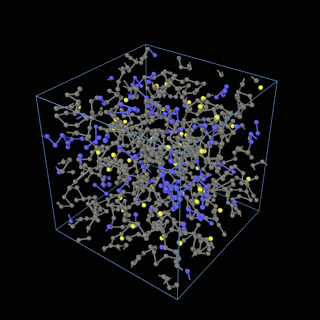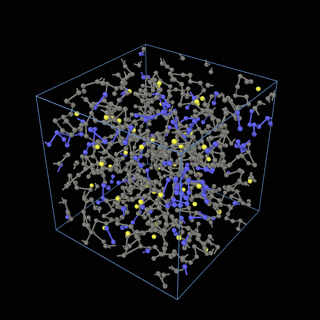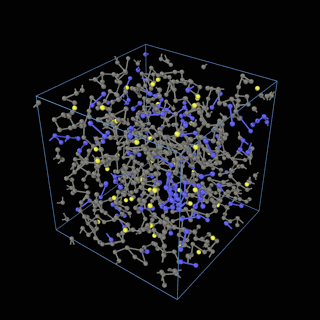
The coarse-graining method we are using is rather simple – a graph clustering algorithm on the atomic structure of the MD system, that groups nearby bonded atoms into CG-beads. There is rich literature on coarse-graining methods for various systems. However, these approaches are usually heuristic-based and system-specific. Many interesting questions can be asked about how to coarse-grain: e.g., given a target property to estimate and a computation budget, what is the best coarse-graining mapping to maximize the estimation accuracy? How to quantify the loss of information in a given coarse-graining? Can we dynamically coarse-grain? i.e., can the coarse-graining mapping evolve with the MD simulation? I am already overwhelmed by possible research directions in an attempt to answer these questions!